Wherein a frustrated businessman is thrust into the harsh light of international industry, and comes to grips with a challenge far greater than himself: The Flag Unions.
What’s this got to do with HUSSAR? Palettes. It’s always palettes.
I’ll paraphrase the problem I posted to Facebook in late 2012:
I own a flag-making business and have an opportunity to make a big haul on a large order, but first I need to prove out my logistics with a smaller run. I’m trying to minimize my costs.
I have two factories (Factory A is in Algeria, and Factory B is in Brazil). Each factory has its own flag-making machine, and each machine can only hold 5 colors of ink. Ink is horrendously expensive, so I’m trying to optimize which ink barrels go to each Factory. Changing ink is also time-consuming and expensive (damn those Brazilian and Algerian unions!), so I want to figure out which factories get which inks in advance. Also due to union rules, a flag must be made at one and only one factory (so no printing half a flag‘s colors in one factory and shipping it to the other to finish).
Ink comes in the following colors:
I’m not allowed to mix inks, again because of those pesky union rules.
A flag consists of between 1 and 5 colors, which is convenient because as stated before, the machines can only hold 5 inks.
Here’s my trial order of flags, and the Factories illustrated:
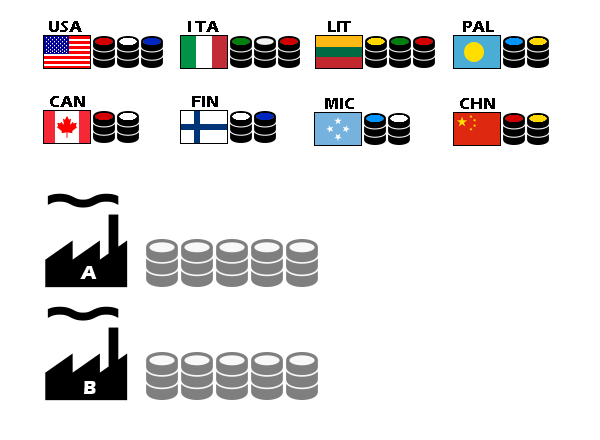
A total of 6 unique colors, more than any one Factory can hold, so we definitely have to split this up!
Here is a possible solution of which inks to send to each factory:
That’s only 8 barrels of ink! Is this the best I can do, though? I’d like an algorithm that could prove that, while running in a reasonable amount of time (preferably in under a couple of seconds).
As mentioned before, this is a trial run for moving up to the big leagues. In the big leagues, I’ll have up to 64 ink choices, my Factory machines will be upgraded to hold 16 inks, and my orders will be up to 512 unique flags with up to 16 colors in each flag. The big-big leagues are 4096 ink choices, and 16 factories!
There are certain heuristics that can be employed, like building a hierarchy (e.g., I know that if I can fit USA, I can certainly fit Canada or Finland as they are proper subsets), or tossing out possible solutions if the number of colors would overflow.
What’s This Really About?
The analogy, as alluded to in the teaser, regards hardware palettes and how to distribute colors of our images across those palettes. As you’ll remember from the previous post, palettes are at a premium in old school hardware, and yet capable of some fantastic effects that can really bring our games alive. We want to maximize our palette usage to allow as many colors onscreen as possible, and to leave room for all those cool tricks.
However, it turns out this is a non-trivial problem to solve: determining how we allocate our images (flags) across the hardware palettes (factories) quickly becomes infeasible. Our worst-case scenarios can easily enter into the billions–or more!–possible combinations. Time to break out the ol’ computer science textbooks.
Brute Force
One very valid approach might be to brute force our way through all of the various combinations. The issue here, of course, is how difficult that winds up being. Let’s consider the facts:
- Each flag must be dedicated to one factory
- No flag can have more colors than a single factory can hold inks
- There are no limits to how many flags will be made at a given factory
With that in mind, each flag could be made at any factory. If we have 8 flags and 2 factories, as in our example, each flag could be made at either factory, or 2×2×2×2×2×2×2×2 = 256 combinations. Extrapolating, we wind up with a simple equation of:
numCombinations = numFactories to the numFlags power.
This is a very reasonable number for our test case. However, on even the Sega Master System (2 palettes, maximum of 448 tiles), this is a whopping 7.268387e+134 combinations. On a system with 4 palettes…well, I’ll let you think about that. This matches the definition of an exponential worst-case scenario: O( c^n ), where c > 1.
Other Factors
As we explore solutions to this problem, let us consider a few additional wrinkles:
- This isn’t a straight-up bin-packing problem, as choosing a flag for a factory doesn’t necessarily add the total colors in the flag to the factory’s roster–there’s often some overlap. Most bin-packing algorithms reduce the space available with each “move.”
- Similarly, this isn’t exactly a knapsack problem, either, although it seems to share many of the same constraints.
- How we calculate the effects of a “move” (i.e., see how many inks a given flag would add) can become computationally expensive. We need efficient algorithms, such as fast union-find structures, to gauge impact.
- At the end of the day, we only need to make exactly numFlags moves, but the effects of each one of those moves will influence future choices.
- We need to look at flags relationships to each other, and not necessarily in the obvious ways. Which flags share most in common with others? Which ones get us the most bang-for-the-buck?
- Is there a way to prove that we can solve this? Are we in the realm of NP-Hard or NP-Complete?
Coming Soon
In the future we’ll be looking into several approaches to the Flag Problem. One solution, suggested by Jason Hughes of Steel Penny Games, set me on a long and winding road through such hallowed names as Skiena and Sedgewick. While I prepare a post about that solution, I’d welcome other thoughts about how to solve this deceptively complex problem!




